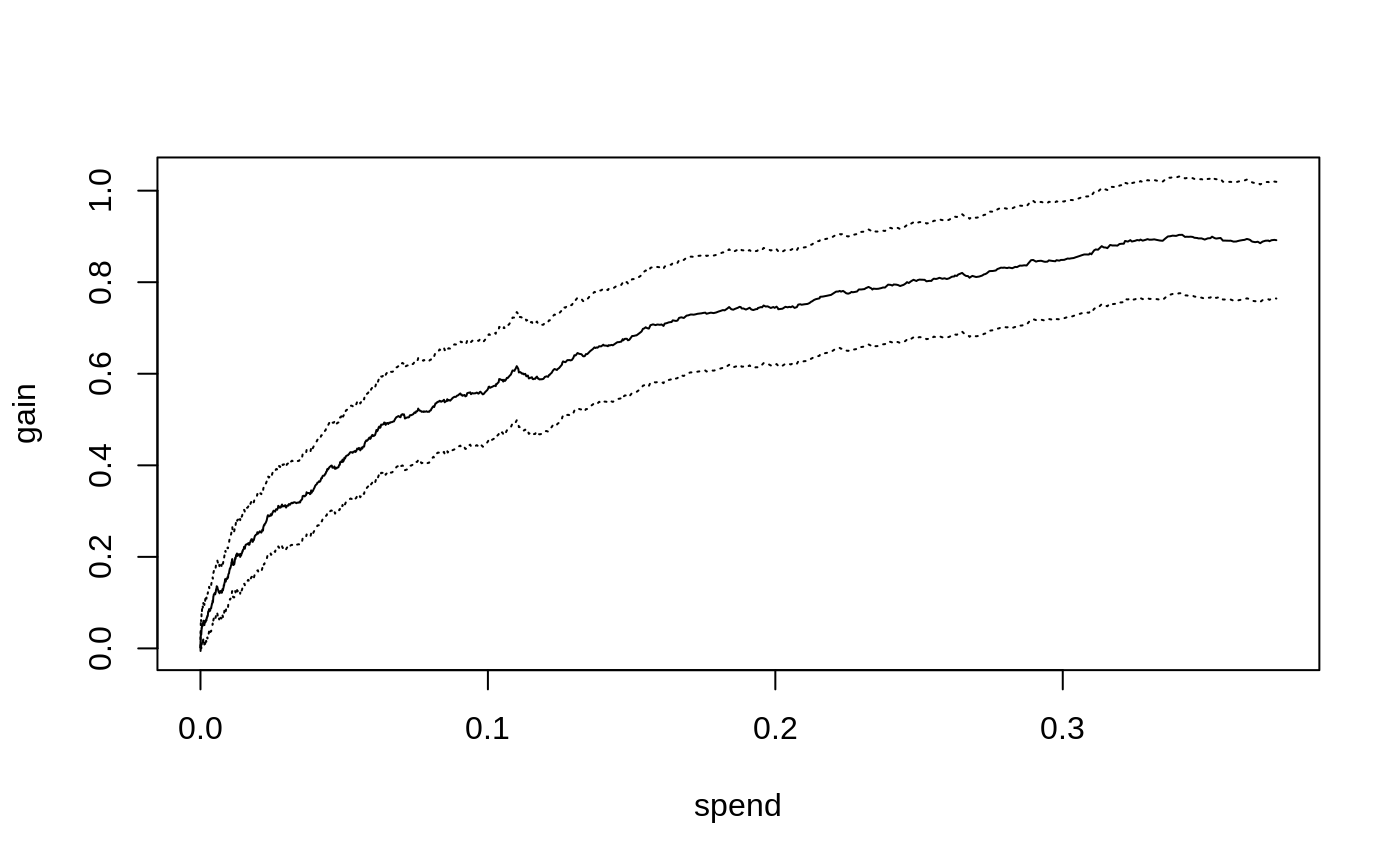
Construct evaluation scores via augmented inverse-propensity weighting.

A simple convenience function to construct an AIPW-based evaluation score given estimates of conditional means and treatment propensities.

get_aipw_scores(Y, W, mu.hat, W.hat = NULL)

Arguments

Y	The observed outcome.
W	The observed treatment assignment (must be a factor vector, where the first factor level is the control arm).
mu.hat	A matrix of conditional mean estimates for each arm, \(E[Y_i | W_i = k, X_i]\).
W.hat	Optional treatment propensities. If these vary by unit and arm, then this should be a matrix with the treatment assignment probability of units to arms, with columns corresponding to the levels of W. If these only vary by arm, a vector can also be supplied. If W.hat is NULL (Default), then the assignment probabilities are assumed to be uniform and the same for each arm.

Value

An \(n \cdot K\) matrix of evaluation scores (eqn (13) in the multi-armed Qini paper).

References

Robins, James M, Andrea Rotnitzky, and Lue Ping Zhao. "Estimation of regression coefficients when some regressors are not always observed." Journal of the American statistical Association, 89(427), 1994.

Sverdrup, Erik, Han Wu, Susan Athey, and Stefan Wager. "Qini Curves for Multi-Armed Treatment Rules". arXiv preprint arXiv:2306.11979, 2023.

Examples

# \donttest{
if (require("grf", quietly = TRUE)) {
# Simulate data with two treatment arms (k = 1, 2) and a control arm (k = 0).
n <- 3000
p <- 5
X <- matrix(runif(n * p), n, p)
W <- as.factor(sample(c("0", "1", "2"), n, replace = TRUE))
Y <- X[, 1] + X[, 2] * (W == "1") + 1.5 * X[, 3] * (W == "2") + rnorm(n)

# Fit a CATE estimator on a training sample.
train <- sample(1:n, n/2)
tau.forest <- grf::multi_arm_causal_forest(X[train, ], Y[train], W[train])

# Predict CATEs on held out evaluation data.
test <- -train
tau.hat <- predict(tau.forest, X[test, ], drop = TRUE)$predictions
# Form costs.
cost <- cbind(X[test, 4] / 4, X[test, 5])

# Estimate nuisance components for test set AIPW scores.
X.test <- X[test, ]
Y.test <- Y[test]
W.test <- W[test]

# Fit models for E[Y | W = k, X], k = 0, 1, 2, using for example separate random forests.
Y0.forest <- grf::regression_forest(X.test[W.test == 0, ], Y.test[W.test == 0])
Y1.forest <- grf::regression_forest(X.test[W.test == 1, ], Y.test[W.test == 1])
Y2.forest <- grf::regression_forest(X.test[W.test == 2, ], Y.test[W.test == 2])
mu.hat = cbind(
   mu0 = predict(Y0.forest, X.test)$predictions,
   mu1 = predict(Y1.forest, X.test)$predictions,
   mu2 = predict(Y2.forest, X.test)$predictions
)

# If unknown, estimate the propensity scores E[W = k | X].
W.hat <- predict(grf::probability_forest(X.test, W.test))$predictions

# Form doubly robust scores.
DR.scores <- get_aipw_scores(Y.test, W.test, mu.hat, W.hat)

# Fit a Qini curve estimated with forest-based AIPW.
qini <- maq(tau.hat, cost, DR.scores, R = 200)
plot(qini)
}
# }