Trains a causal forest that can be used to estimate conditional average treatment effects tau(X). When the treatment assignment W is binary and unconfounded, we have tau(X) = E[Y(1) - Y(0) | X = x], where Y(0) and Y(1) are potential outcomes corresponding to the two possible treatment states. When W is continuous, we effectively estimate an average partial effect Cov[Y, W | X = x] / Var[W | X = x], and interpret it as a treatment effect given unconfoundedness.
causal_forest( X, Y, W, Y.hat = NULL, W.hat = NULL, num.trees = 2000, sample.weights = NULL, clusters = NULL, equalize.cluster.weights = FALSE, sample.fraction = 0.5, mtry = min(ceiling(sqrt(ncol(X)) + 20), ncol(X)), min.node.size = 5, honesty = TRUE, honesty.fraction = 0.5, honesty.prune.leaves = TRUE, alpha = 0.05, imbalance.penalty = 0, stabilize.splits = TRUE, ci.group.size = 2, tune.parameters = "none", tune.num.trees = 200, tune.num.reps = 50, tune.num.draws = 1000, compute.oob.predictions = TRUE, num.threads = NULL, seed = runif(1, 0, .Machine$integer.max) )
Arguments
| X | The covariates used in the causal regression. |
|---|---|
| Y | The outcome (must be a numeric vector with no NAs). |
| W | The treatment assignment (must be a binary or real numeric vector with no NAs). |
| Y.hat | Estimates of the expected responses E[Y | Xi], marginalizing over treatment. If Y.hat = NULL, these are estimated using a separate regression forest. See section 6.1.1 of the GRF paper for further discussion of this quantity. Default is NULL. |
| W.hat | Estimates of the treatment propensities E[W | Xi]. If W.hat = NULL, these are estimated using a separate regression forest. Default is NULL. |
| num.trees | Number of trees grown in the forest. Note: Getting accurate confidence intervals generally requires more trees than getting accurate predictions. Default is 2000. |
| sample.weights | Weights given to each sample in estimation. If NULL, each observation receives the same weight. Note: To avoid introducing confounding, weights should be independent of the potential outcomes given X. Default is NULL. |
| clusters | Vector of integers or factors specifying which cluster each observation corresponds to. Default is NULL (ignored). |
| equalize.cluster.weights | If FALSE, each unit is given the same weight (so that bigger clusters get more weight). If TRUE, each cluster is given equal weight in the forest. In this case, during training, each tree uses the same number of observations from each drawn cluster: If the smallest cluster has K units, then when we sample a cluster during training, we only give a random K elements of the cluster to the tree-growing procedure. When estimating average treatment effects, each observation is given weight 1/cluster size, so that the total weight of each cluster is the same. Note that, if this argument is FALSE, sample weights may also be directly adjusted via the sample.weights argument. If this argument is TRUE, sample.weights must be set to NULL. Default is FALSE. |
| sample.fraction | Fraction of the data used to build each tree. Note: If honesty = TRUE, these subsamples will further be cut by a factor of honesty.fraction. Default is 0.5. |
| mtry | Number of variables tried for each split. Default is \(\sqrt p + 20\) where p is the number of variables. |
| min.node.size | A target for the minimum number of observations in each tree leaf. Note that nodes with size smaller than min.node.size can occur, as in the original randomForest package. Default is 5. |
| honesty | Whether to use honest splitting (i.e., sub-sample splitting). Default is TRUE. For a detailed description of honesty, honesty.fraction, honesty.prune.leaves, and recommendations for parameter tuning, see the grf algorithm reference. |
| honesty.fraction | The fraction of data that will be used for determining splits if honesty = TRUE. Corresponds to set J1 in the notation of the paper. Default is 0.5 (i.e. half of the data is used for determining splits). |
| honesty.prune.leaves | If TRUE, prunes the estimation sample tree such that no leaves are empty. If FALSE, keep the same tree as determined in the splits sample (if an empty leave is encountered, that tree is skipped and does not contribute to the estimate). Setting this to FALSE may improve performance on small/marginally powered data, but requires more trees (note: tuning does not adjust the number of trees). Only applies if honesty is enabled. Default is TRUE. |
| alpha | A tuning parameter that controls the maximum imbalance of a split. Default is 0.05. |
| imbalance.penalty | A tuning parameter that controls how harshly imbalanced splits are penalized. Default is 0. |
| stabilize.splits | Whether or not the treatment should be taken into account when determining the imbalance of a split. Default is TRUE. |
| ci.group.size | The forest will grow ci.group.size trees on each subsample. In order to provide confidence intervals, ci.group.size must be at least 2. Default is 2. |
| tune.parameters | A vector of parameter names to tune. If "all": all tunable parameters are tuned by cross-validation. The following parameters are tunable: ("sample.fraction", "mtry", "min.node.size", "honesty.fraction", "honesty.prune.leaves", "alpha", "imbalance.penalty"). If honesty is FALSE the honesty.* parameters are not tuned. Default is "none" (no parameters are tuned). |
| tune.num.trees | The number of trees in each 'mini forest' used to fit the tuning model. Default is 200. |
| tune.num.reps | The number of forests used to fit the tuning model. Default is 50. |
| tune.num.draws | The number of random parameter values considered when using the model to select the optimal parameters. Default is 1000. |
| compute.oob.predictions | Whether OOB predictions on training set should be precomputed. Default is TRUE. |
| num.threads | Number of threads used in training. By default, the number of threads is set to the maximum hardware concurrency. |
| seed | The seed of the C++ random number generator. |
Value
A trained causal forest object. If tune.parameters is enabled, then tuning information will be included through the `tuning.output` attribute.
References
Athey, Susan, Julie Tibshirani, and Stefan Wager. "Generalized Random Forests". Annals of Statistics, 47(2), 2019.
Wager, Stefan, and Susan Athey. "Estimation and Inference of Heterogeneous Treatment Effects using Random Forests". Journal of the American Statistical Association, 113(523), 2018.
Nie, Xinkun, and Stefan Wager. "Quasi-Oracle Estimation of Heterogeneous Treatment Effects". Biometrika, 108(2), 2021.
Examples
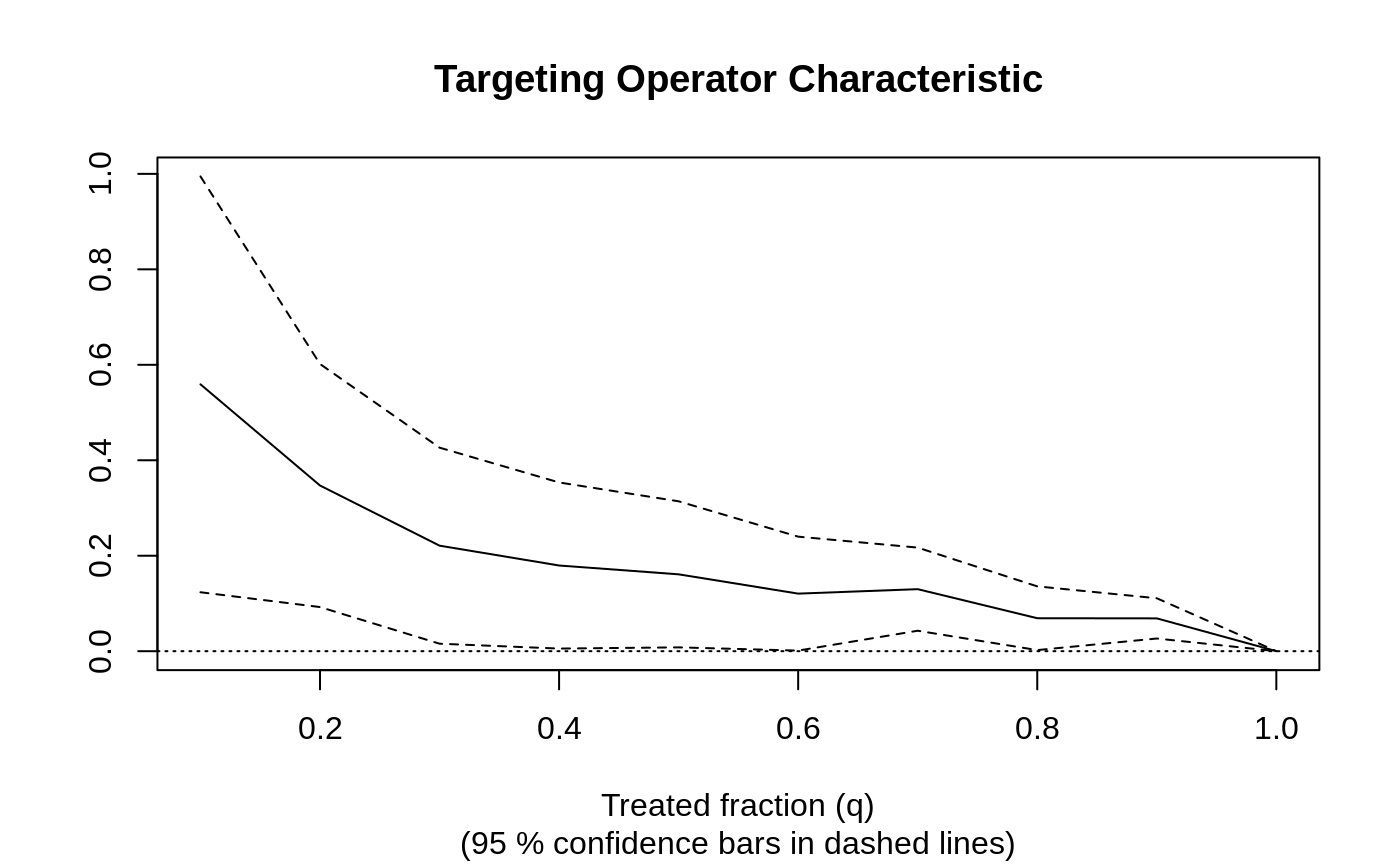
# \donttest{ # Train a causal forest. n <- 500 p <- 10 X <- matrix(rnorm(n * p), n, p) W <- rbinom(n, 1, 0.5) Y <- pmax(X[, 1], 0) * W + X[, 2] + pmin(X[, 3], 0) + rnorm(n) c.forest <- causal_forest(X, Y, W) # Predict using the forest. X.test <- matrix(0, 101, p) X.test[, 1] <- seq(-2, 2, length.out = 101) c.pred <- predict(c.forest, X.test) # Predict on out-of-bag training samples. c.pred <- predict(c.forest) # Predict with confidence intervals; growing more trees is now recommended. c.forest <- causal_forest(X, Y, W, num.trees = 4000) c.pred <- predict(c.forest, X.test, estimate.variance = TRUE) # In some examples, pre-fitting models for Y and W separately may # be helpful (e.g., if different models use different covariates). # In some applications, one may even want to get Y.hat and W.hat # using a completely different method (e.g., boosting). n <- 2000 p <- 20 X <- matrix(rnorm(n * p), n, p) TAU <- 1 / (1 + exp(-X[, 3])) W <- rbinom(n, 1, 1 / (1 + exp(-X[, 1] - X[, 2]))) Y <- pmax(X[, 2] + X[, 3], 0) + rowMeans(X[, 4:6]) / 2 + W * TAU + rnorm(n) forest.W <- regression_forest(X, W, tune.parameters = "all") W.hat <- predict(forest.W)$predictions forest.Y <- regression_forest(X, Y, tune.parameters = "all") Y.hat <- predict(forest.Y)$predictions forest.Y.varimp <- variable_importance(forest.Y) # Note: Forests may have a hard time when trained on very few variables # (e.g., ncol(X) = 1, 2, or 3). We recommend not being too aggressive # in selection. selected.vars <- which(forest.Y.varimp / mean(forest.Y.varimp) > 0.2) tau.forest <- causal_forest(X[, selected.vars], Y, W, W.hat = W.hat, Y.hat = Y.hat, tune.parameters = "all" ) tau.hat <- predict(tau.forest)$predictions # See if a causal forest succeeded in capturing heterogeneity by plotting # the TOC and calculating a 95% CI for the AUTOC. train <- sample(1:n, n / 2) train.forest <- causal_forest(X[train, ], Y[train], W[train]) eval.forest <- causal_forest(X[-train, ], Y[-train], W[-train]) rate <- rank_average_treatment_effect(eval.forest, predict(train.forest, X[-train, ])$predictions) plot(rate)#> [1] "AUTOC: 0.22 +/ 0.15"# }