Trains a causal survival forest that can be used to estimate conditional treatment effects tau(X) with right-censored outcomes. We estimate either 1) tau(X) = E[min(T(1), horizon) - min(T(0), horizon) | X = x], where T(1) and T(0) are potental outcomes corresponding to the two possible treatment states and `horizon` is the maximum follow-up time, or 2) tau(X) = P[T(1) > horizon | X = x] - P[T(0) > horizon | X = x], for a chosen time point `horizon`.
causal_survival_forest( X, Y, W, D, W.hat = NULL, target = c("RMST", "survival.probability"), horizon = NULL, failure.times = NULL, num.trees = 2000, sample.weights = NULL, clusters = NULL, equalize.cluster.weights = FALSE, sample.fraction = 0.5, mtry = min(ceiling(sqrt(ncol(X)) + 20), ncol(X)), min.node.size = 5, honesty = TRUE, honesty.fraction = 0.5, honesty.prune.leaves = TRUE, alpha = 0.05, imbalance.penalty = 0, stabilize.splits = TRUE, ci.group.size = 2, tune.parameters = "none", compute.oob.predictions = TRUE, fast.logrank = FALSE, num.threads = NULL, seed = runif(1, 0, .Machine$integer.max) )
Arguments
| X | The covariates. |
|---|---|
| Y | The event time (must be non-negative). |
| W | The treatment assignment (must be a binary or real numeric vector with no NAs). |
| D | The event type (0: censored, 1: failure/observed event). |
| W.hat | Estimates of the treatment propensities E[W | X = x]. If W.hat = NULL, these are estimated using a separate regression forest. Default is NULL. |
| target | The target estimand. Choices are Restricted Mean Survival Time ("RMST") which estimates 1) E[min(T(1), horizon) - min(T(0), horizon) | X = x], or "survival.probability" which estimates 2) P[T(1) > horizon | X = x] - P[T(0) > horizon | X = x]. Default is "RMST". |
| horizon | A scalar that defines the estimand (required). If target is "RMST" then this defines the maximum follow-up time. If target is "survival.probability", then this defines the time point for the absolute risk difference estimate. |
| failure.times | A vector of event times to fit the survival curves at. If NULL, then all the unique event times are used. This speeds up forest estimation by constraining the event grid. Observed event times are rounded down to the last sorted occurance less than or equal to the specified failure time. The time points should be in increasing order. Default is NULL. |
| num.trees | Number of trees grown in the forest. Note: Getting accurate confidence intervals generally requires more trees than getting accurate predictions. Default is 2000. |
| sample.weights | Weights given to each sample in estimation. If NULL, each observation receives the same weight. Note: To avoid introducing confounding, weights should be independent of the potential outcomes given X. Sample weights are not used in survival spliting. Default is NULL. |
| clusters | Vector of integers or factors specifying which cluster each observation corresponds to. Default is NULL (ignored). |
| equalize.cluster.weights | If FALSE, each unit is given the same weight (so that bigger clusters get more weight). If TRUE, each cluster is given equal weight in the forest. In this case, during training, each tree uses the same number of observations from each drawn cluster: If the smallest cluster has K units, then when we sample a cluster during training, we only give a random K elements of the cluster to the tree-growing procedure. When estimating average treatment effects, each observation is given weight 1/cluster size, so that the total weight of each cluster is the same. Note that, if this argument is FALSE, sample weights may also be directly adjusted via the sample.weights argument. If this argument is TRUE, sample.weights must be set to NULL. Default is FALSE. |
| sample.fraction | Fraction of the data used to build each tree. Note: If honesty = TRUE, these subsamples will further be cut by a factor of honesty.fraction. Default is 0.5. |
| mtry | Number of variables tried for each split. Default is \(\sqrt p + 20\) where p is the number of variables. |
| min.node.size | A target for the minimum number of observations in each tree leaf. Note that nodes with size smaller than min.node.size can occur, as in the original randomForest package. Default is 5. |
| honesty | Whether to use honest splitting (i.e., sub-sample splitting). Default is TRUE. For a detailed description of honesty, honesty.fraction, honesty.prune.leaves, and recommendations for parameter tuning, see the grf algorithm reference. |
| honesty.fraction | The fraction of data that will be used for determining splits if honesty = TRUE. Corresponds to set J1 in the notation of the paper. Default is 0.5 (i.e. half of the data is used for determining splits). |
| honesty.prune.leaves | If TRUE, prunes the estimation sample tree such that no leaves are empty. If FALSE, keep the same tree as determined in the splits sample (if an empty leave is encountered, that tree is skipped and does not contribute to the estimate). Setting this to FALSE may improve performance on small/marginally powered data, but requires more trees (note: tuning does not adjust the number of trees). Only applies if honesty is enabled. Default is TRUE. |
| alpha | A tuning parameter that controls the maximum imbalance of a split. This parameter plays the same role as in causal forest and survival forest, where for the latter the number of failures in each child has to be at least one or `alpha` times the number of samples in the parent node. Default is 0.05. (On data with very low event rate the default value may be too high for the forest to split and lowering it may be beneficial). |
| imbalance.penalty | A tuning parameter that controls how harshly imbalanced splits are penalized. Default is 0. |
| stabilize.splits | Whether or not the treatment and censoring status should be taken into account when determining the imbalance of a split. The requirement for valid split candidates is the same as in causal_forest with the additional constraint that num.failures(child) >= num.samples(parent) * alpha. Default is TRUE. |
| ci.group.size | The forest will grow ci.group.size trees on each subsample. In order to provide confidence intervals, ci.group.size must be at least 2. Default is 2. |
| tune.parameters | (Currently only applies to the regression forest used in W.hat estimation) A vector of parameter names to tune. If "all": all tunable parameters are tuned by cross-validation. The following parameters are tunable: ("sample.fraction", "mtry", "min.node.size", "honesty.fraction", "honesty.prune.leaves", "alpha", "imbalance.penalty"). If honesty is FALSE the honesty.* parameters are not tuned. Default is "none" (no parameters are tuned). |
| compute.oob.predictions | Whether OOB predictions on training set should be precomputed. Default is TRUE. |
| fast.logrank | Whether to use the `fast.logrank` option when estimating censoring corrections with `survival_forest`. Default is FALSE. |
| num.threads | Number of threads used in training. By default, the number of threads is set to the maximum hardware concurrency. |
| seed | The seed of the C++ random number generator. |
Value
A trained causal_survival_forest forest object.
Details
When W is continuous, we effectively estimate an average partial effect corresponding to 1) Cov[min(T, horizon), W | X = x] / Var[W | X = x] or 2) Cov[1(T > horizon), W | X = x] / Var[W | X = x], and interpret it as a treatment effect given unconfoundedness.
References
Cui, Yifan, Michael R. Kosorok, Erik Sverdrup, Stefan Wager, and Ruoqing Zhu. "Estimating Heterogeneous Treatment Effects with Right-Censored Data via Causal Survival Forests". Journal of the Royal Statistical Society: Series B, 85(2), 2023.
Sverdrup, Erik, and Stefan Wager. "Treatment Heterogeneity with Right-Censored Outcomes Using grf". ASA Lifetime Data Science Newsletter, January 2024 (arXiv:2312.02482).
Examples
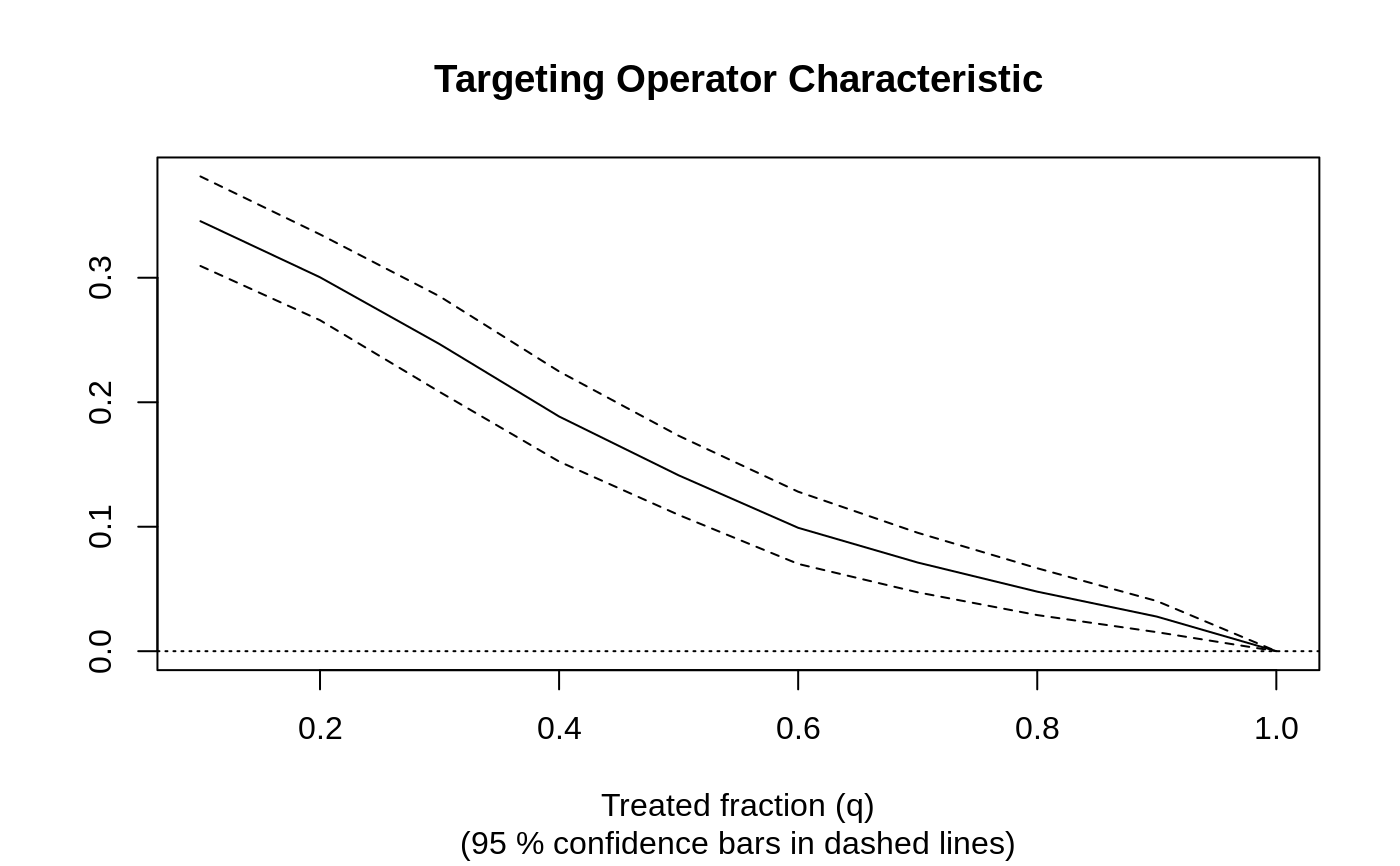
# \donttest{ # Train a causal survival forest targeting a Restricted Mean Survival Time (RMST) # with maximum follow-up time set to `horizon`. n <- 2000 p <- 5 X <- matrix(runif(n * p), n, p) W <- rbinom(n, 1, 0.5) horizon <- 1 failure.time <- pmin(rexp(n) * X[, 1] + W, horizon) censor.time <- 2 * runif(n) Y <- pmin(failure.time, censor.time) D <- as.integer(failure.time <= censor.time) # Save computation time by constraining the event grid by discretizing (rounding) continuous events. cs.forest <- causal_survival_forest(X, round(Y, 2), W, D, horizon = horizon) # Or do so more flexibly by defining your own time grid using the failure.times argument. # grid <- seq(min(Y), max(Y), length.out = 150) # cs.forest <- causal_survival_forest(X, Y, W, D, horizon = horizon, failure.times = grid) # Predict using the forest. X.test <- matrix(0.5, 10, p) X.test[, 1] <- seq(0, 1, length.out = 10) cs.pred <- predict(cs.forest, X.test) # Predict on out-of-bag training samples. cs.pred <- predict(cs.forest) # Predict with confidence intervals; growing more trees is now recommended. c.pred <- predict(cs.forest, X.test, estimate.variance = TRUE) # Compute a doubly robust estimate of the average treatment effect. average_treatment_effect(cs.forest)#> estimate std.err #> 0.61260462 0.01093297# Compute the best linear projection on the first covariate. best_linear_projection(cs.forest, X[, 1])#> #> Best linear projection of the conditional average treatment effect. #> Confidence intervals are cluster- and heteroskedasticity-robust (HC3): #> #> Estimate Std. Error t value Pr(>|t|) #> (Intercept) 0.902477 0.014417 62.599 < 2.2e-16 *** #> A1 -0.571627 0.031880 -17.930 < 2.2e-16 *** #> --- #> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 #># See if a causal survival forest succeeded in capturing heterogeneity by plotting # the TOC and calculating a 95% CI for the AUTOC. train <- sample(1:n, n / 2) eval <- -train train.forest <- causal_survival_forest(X[train, ], Y[train], W[train], D[train], horizon = horizon) eval.forest <- causal_survival_forest(X[eval, ], Y[eval], W[eval], D[eval], horizon = horizon) rate <- rank_average_treatment_effect(eval.forest, predict(train.forest, X[eval, ])$predictions) plot(rate)#> [1] "AUTOC: 0.16 +/ 0.02"# }