Predict with a causal survival forest forest

Gets estimates of tau(X) using a trained causal survival forest.

# S3 method for causal_survival_forest
predict(
  object,
  newdata = NULL,
  num.threads = NULL,
  estimate.variance = FALSE,
  ...
)

Arguments

object	The trained forest.
newdata	Points at which predictions should be made. If NULL, makes out-of-bag predictions on the training set instead (i.e., provides predictions at Xi using only trees that did not use the i-th training example). Note that this matrix should have the number of columns as the training matrix, and that the columns must appear in the same order.
num.threads	Number of threads used in prediction. If set to NULL, the software automatically selects an appropriate amount.
estimate.variance	Whether variance estimates for \(\hat\tau(x)\) are desired (for confidence intervals).
...	Additional arguments (currently ignored).

Value

Vector of predictions along with optional variance estimates.

Examples

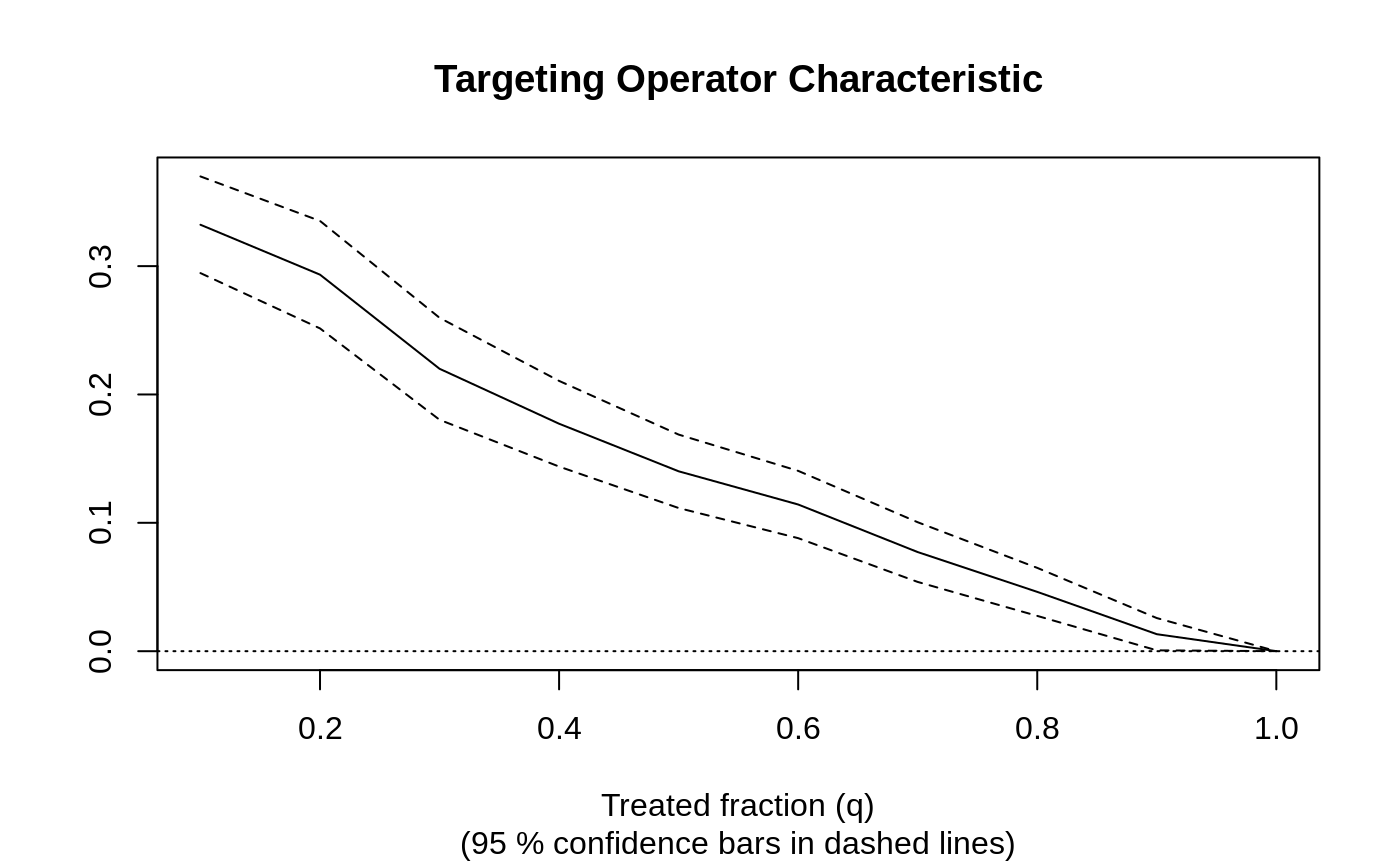
# \donttest{
# Train a causal survival forest targeting a Restricted Mean Survival Time (RMST)
# with maximum follow-up time set to `horizon`.
n <- 2000
p <- 5
X <- matrix(runif(n * p), n, p)
W <- rbinom(n, 1, 0.5)
horizon <- 1
failure.time <- pmin(rexp(n) * X[, 1] + W, horizon)
censor.time <- 2 * runif(n)
Y <- pmin(failure.time, censor.time)
D <- as.integer(failure.time <= censor.time)
# Save computation time by constraining the event grid by discretizing (rounding) continuous events.
cs.forest <- causal_survival_forest(X, round(Y, 2), W, D, horizon = horizon)
# Or do so more flexibly by defining your own time grid using the failure.times argument.
# grid <- seq(min(Y), max(Y), length.out = 150)
# cs.forest <- causal_survival_forest(X, Y, W, D, horizon = horizon, failure.times = grid)

# Predict using the forest.
X.test <- matrix(0.5, 10, p)
X.test[, 1] <- seq(0, 1, length.out = 10)
cs.pred <- predict(cs.forest, X.test)

# Predict on out-of-bag training samples.
cs.pred <- predict(cs.forest)

# Predict with confidence intervals; growing more trees is now recommended.
c.pred <- predict(cs.forest, X.test, estimate.variance = TRUE)

# Compute a doubly robust estimate of the average treatment effect.
average_treatment_effect(cs.forest)
#>   estimate    std.err 
#> 0.61852926 0.01107368 

# Compute the best linear projection on the first covariate.
best_linear_projection(cs.forest, X[, 1])
#> 
#> Best linear projection of the conditional average treatment effect.
#> Confidence intervals are cluster- and heteroskedasticity-robust (HC3):
#> 
#>              Estimate Std. Error t value  Pr(>|t|)    
#> (Intercept)  0.908994   0.014771  61.539 < 2.2e-16 ***
#> A1          -0.581941   0.033681 -17.278 < 2.2e-16 ***
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#> 

# See if a causal survival forest succeeded in capturing heterogeneity by plotting
# the TOC and calculating a 95% CI for the AUTOC.
train <- sample(1:n, n / 2)
eval <- -train
train.forest <- causal_survival_forest(X[train, ], Y[train], W[train], D[train], horizon = horizon)
eval.forest <- causal_survival_forest(X[eval, ], Y[eval], W[eval], D[eval], horizon = horizon)
rate <- rank_average_treatment_effect(eval.forest,
                                      predict(train.forest, X[eval, ])$predictions)
plot(rate)
paste("AUTOC:", round(rate$estimate, 2), "+/", round(1.96 * rate$std.err, 2))
#> [1] "AUTOC: 0.16 +/ 0.02"
# }